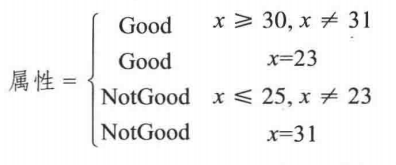支持向量机SVM(Support Vector Machine)是一种用来进行模式识别、分类、回归的机器学习模型。
SVM原理描述
模型表示
客户信息数轴表示如下所示:
以数学表达式对上述信息进行描述,可以用下式进行表示:
然而该方法对于大型数据集容易发生拟合,且过于复杂。
因此可以忽略一些点,进行一刀切,如下所示:
但是该方法容易导致错分率高。因此SVM就是找一种方式正确的描述分类方程。
超平面
因此该超平面的公式可以用下式进行表示:
\[g(v)=wv+b
\]
其中v是样本向量,在二维空间v=(x,y),在三维空间v=(x,y,z)。w是参数向量,在二维空间w=(A,B),在三维空间w=(A,B,C)。
因此上述距离公式可以表示为:
\[d(v)=|g(v)|/\left \| w \right \|
\]
超平面确定
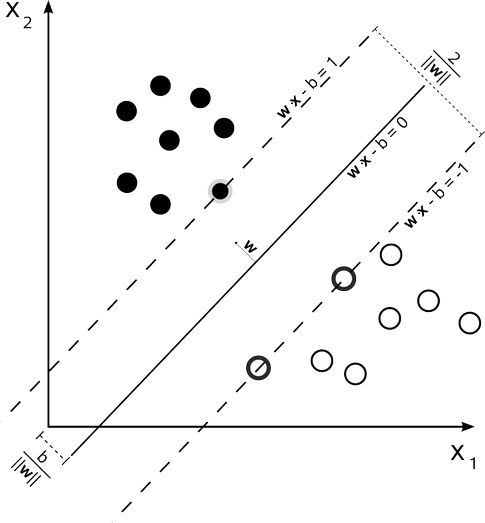
SVM目标是找到一个超平面,使得其在两个类中间分开。并使得该超平面到两边的距离最大,如下图所示:
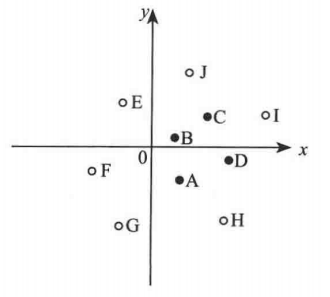
但是如果对于线性不可分的情况,如下图所示:
此时上述方式无法确定超平面。在SVM在则是通过升维的方式解决。例如:
因此SVM在一维空间上解决线性不可分割的问题是把函数映射到二维空间。同样在n维空间的线性不可分割问题映射到n+1维空间。而这种映射分类函数,在svm用核函数(kernel)进行构造。
sklearn实现
在sklearn支持向量机主要用SVC类支持。SVC所支持的和函数有linear(线性和函数)、rbf(径向基核函数)、sigmoid(神经元激活函数)等,通常推荐使用rbf函数。以客户评价为例代码如下:
from sklearn import svm
import numpy as np
#年龄
X = np.array([[34, 33, 32, 31, 30, 30, 25, 23, 22, 18]])
X = X.T
#质量
y = [1, 0, 1, 0, 1, 1, 0, 1, 0, 1]
clf = svm.SVC(kernel='rbf').fit(X, y)
p = [[30]]
print(clf.predict(p)) #1
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 [email protected] 举报,一经查实,本站将立刻删除。